Photo AI
Figure 3 shows a sketch of part of the curve C with equation y = \frac{1}{2}x + 27 - \frac{12}{x}, \quad x > 0 The point A lies on C and has coordinates \left( 3, -\frac{3}{2} \right) - Edexcel - A-Level Maths Pure - Question 2 - 2018 - Paper 1
Question 2
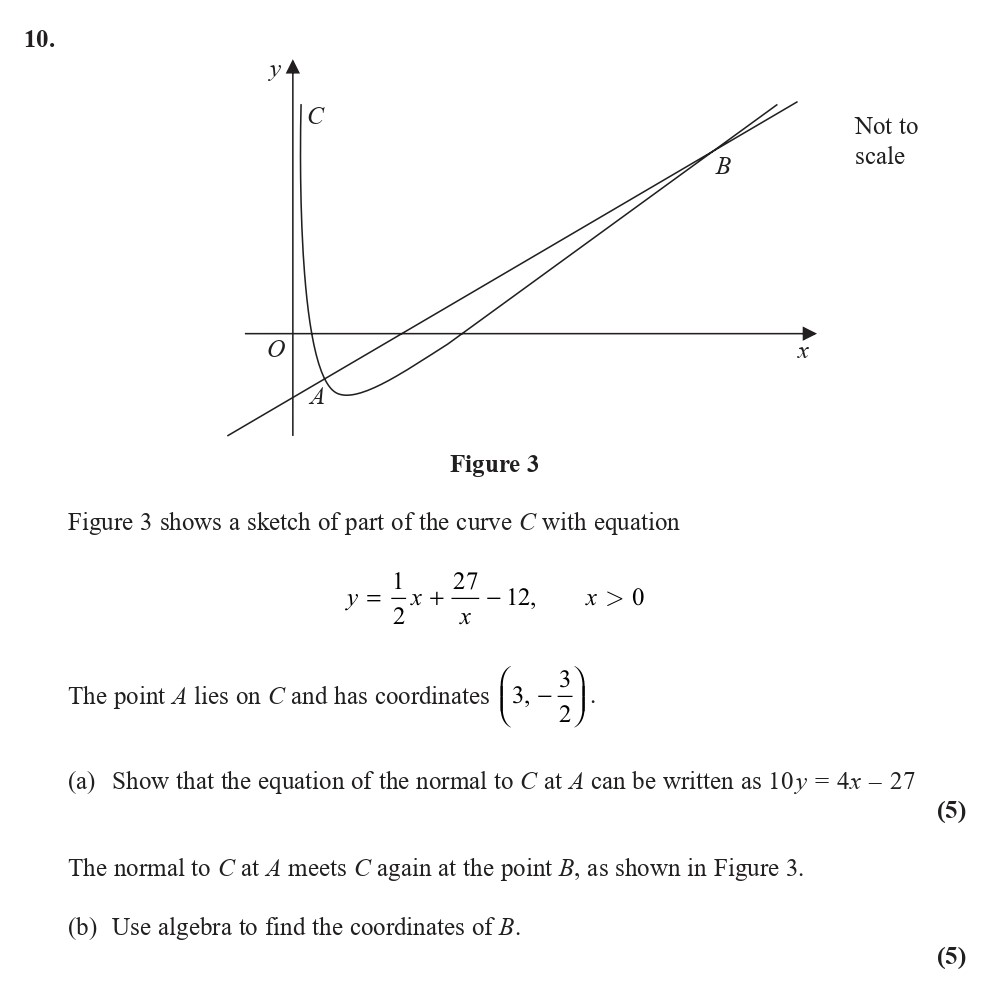
Figure 3 shows a sketch of part of the curve C with equation y = \frac{1}{2}x + 27 - \frac{12}{x}, \quad x > 0 The point A lies on C and has coordinates \left( 3, ... show full transcript
Worked Solution & Example Answer:Figure 3 shows a sketch of part of the curve C with equation y = \frac{1}{2}x + 27 - \frac{12}{x}, \quad x > 0 The point A lies on C and has coordinates \left( 3, -\frac{3}{2} \right) - Edexcel - A-Level Maths Pure - Question 2 - 2018 - Paper 1
Step 1
Show that the equation of the normal to C at A can be written as 10y = 4x - 27.
Answer
To find the equation of the normal at point A, we first need to determine the slope of the tangent line at A.
-
Calculate the derivative: [ y' = \frac{d}{dx} \left( \frac{1}{2}x + 27 - \frac{12}{x} \right) = \frac{1}{2} + \frac{12}{x^2} ]
Substituting the x-coordinate of point A, which is 3, into the derivative:
[ m_t = y'(3) = \frac{1}{2} + \frac{12}{3^2} = \frac{1}{2} + \frac{12}{9} = \frac{1}{2} + \frac{4}{3} = \frac{3}{6} + \frac{8}{6} = \frac{11}{6} ] -
Determine the slope of the normal line: The slope of the normal line ( m_n ) is given by the negative reciprocal of the tangent slope:
[ m_n = -\frac{1}{m_t} = -\frac{6}{11} ] -
Use point-slope form to find the equation of the normal line:
Using point A ( (3, -\frac{3}{2}) ):
[ y - \left(-\frac{3}{2}\right) = -\frac{6}{11} \left(x - 3\right) ]
Simplifying this gives:
[ y + \frac{3}{2} = -\frac{6}{11}x + \frac{18}{11} ]
Multiplying through by 11 to eliminate fractions:
[ 11y + 33 = -6x + 18 ]
Rearranging yields:
[ 6x + 11y = -15 ] Rearranging to get it in the format 10y = 4x - 27 gives us:
[ 10y = 4x - 27. ]
Step 2
Use algebra to find the coordinates of B.
Answer
To find the coordinates of point B where the normal intersects the curve again, we need to set the equations equal:
- Use the curve equation to substitute:
We have:
[ y = \frac{1}{2}x + 27 - \frac{12}{x} ]
and from the previous step:
[ 10y = 4x - 27 ]
Substituting the expression of y from the curve into the normal's equation leads to:
[ 10\left(\frac{1}{2}x + 27 - \frac{12}{x}\right) = 4x - 27 ]
2. Clear the equation of fractions:
Multiplying through by x:
[ 5x + 270 - 120 = 4x^2 - 27x ]
Rearranging gives us:
[ 4x^2 - 32x - 150 = 0 ]
3. Solve the quadratic equation:
Applying the quadratic formula:
[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{32 \pm \sqrt{(-32)^2 - 4(4)(-150)}}{2(4)} ]
This simplifies to:
[ x = \frac{32 \pm \sqrt{1024 + 2400}}{8} = \frac{32 \pm \sqrt{3424}}{8} = \frac{32 \pm 58.5}{8} ]
Solving gives us two values for x. Plug each x-value back into the curve equation to find the corresponding y-values.
