Photo AI
The points A(1, 7), B(20, 7) and C(p, q) form the vertices of a triangle ABC, as shown in Figure 2 - Edexcel - A-Level Maths Pure - Question 9 - 2005 - Paper 2
Question 9
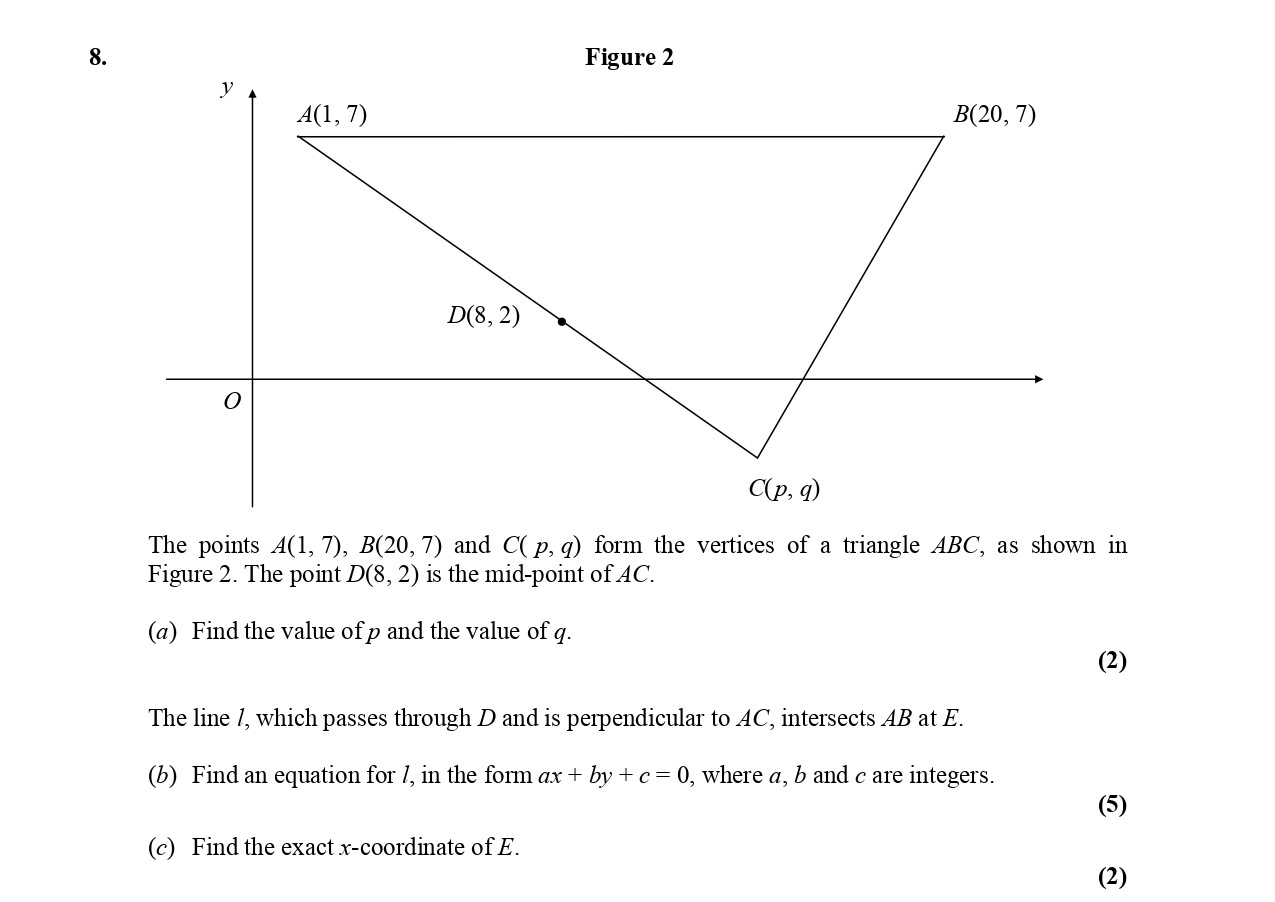
The points A(1, 7), B(20, 7) and C(p, q) form the vertices of a triangle ABC, as shown in Figure 2. The point D(8, 2) is the mid-point of AC. (a) Find the value of ... show full transcript
Worked Solution & Example Answer:The points A(1, 7), B(20, 7) and C(p, q) form the vertices of a triangle ABC, as shown in Figure 2 - Edexcel - A-Level Maths Pure - Question 9 - 2005 - Paper 2
Step 1
Find the value of p and the value of q.
Answer
To find the coordinates (p, q) of point C, we first note that D(8, 2) is the midpoint of AC. Therefore, using the midpoint formula:
We can set up two equations based on the coordinates of points A and C:
-
For x-coordinates: Solving this gives:
-
For y-coordinates: Solving this gives:
Thus, we find that:
- p = 15
- q = -3
Step 2
The line l, which passes through D and is perpendicular to AC, intersects AB at E.
Answer
To determine the gradient of line AC, we first compute the gradient using the coordinates of A(1, 7) and C(15, -3):
The gradient of line l, which is perpendicular to AC, can be found using the negative reciprocal:
Now using point-slope form to find the equation of line l, which passes through point D(8, 2):
Substituting in the values gives:
To convert to standard form, rearranging yields:
Step 3
Find the exact x-coordinate of E.
Answer
To find the x-coordinate at point E where line l intersects AB, we first note that line AB is horizontal (since both A and B have the same y-coordinate of 7). Thus, the equation of line AB is simply:
Substituting this into the equation of line l:
This simplifies to:
Thus, the exact x-coordinate of E is:
