Figure 1 shows a sketch of the curve with equation $y = f(x)$. The curve crosses the x-axis at the points $(1, 0)$ and $(4, 0)$. The maximum point on the curve is $(2, 5)$. In separate diagrams sketch the curves with the following equations. On each diagram show clearly the coordinates of the maximum point and of each point at which the curve crosses the x-axis. a) $y = 2f(x)$. b) $y = f(-x)$. c) Write down the value of the constant $a$.

A-Level Edexcel Maths Pure Quadratics: Figure 1 shows a sketch of the c

Figure 1 shows a sketch of the curve with equation $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 8 - 2008 - Paper 2

Question 8

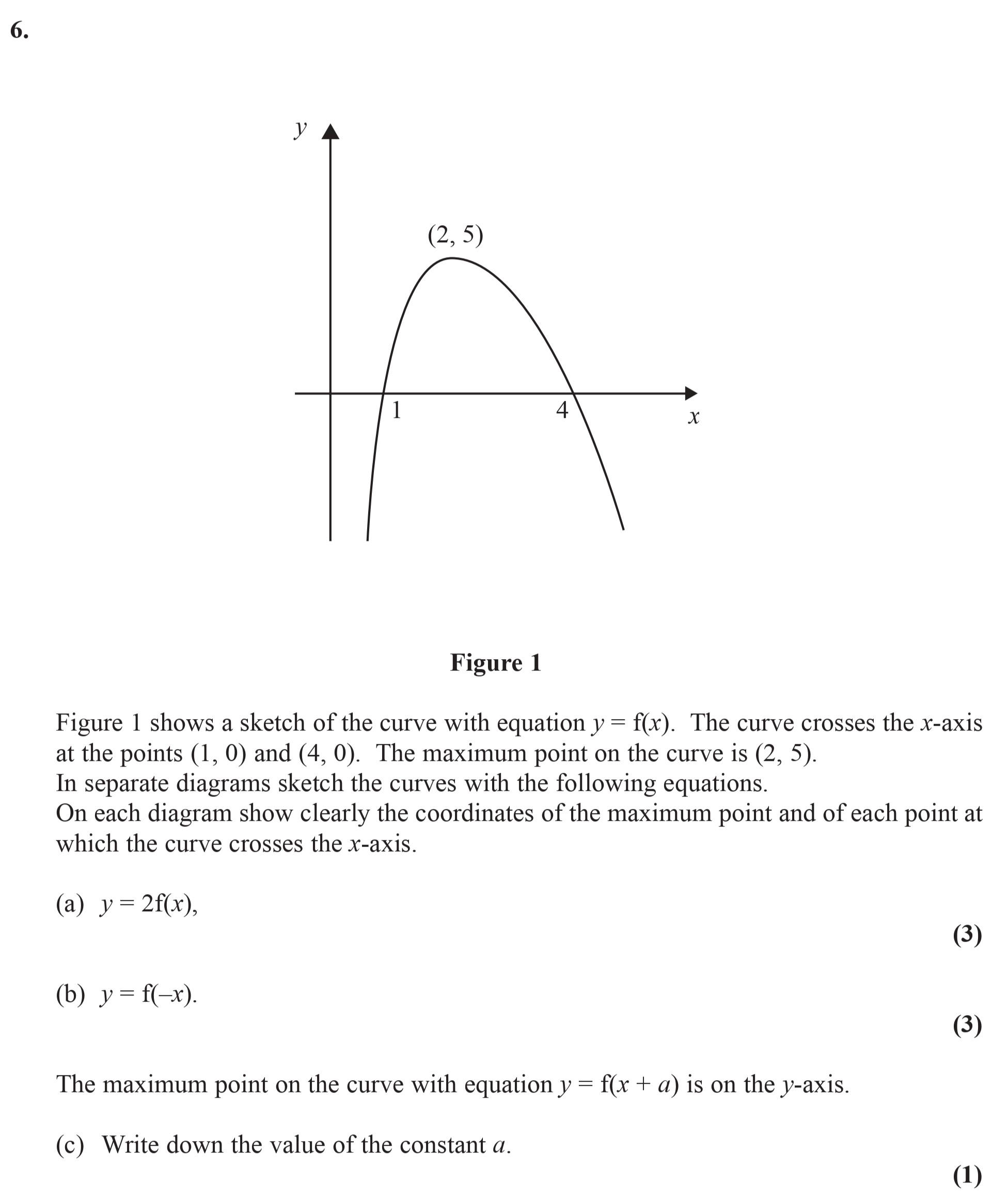
Figure 1 shows a sketch of the curve with equation $y = f(x)$. The curve crosses the x-axis at the points $(1, 0)$ and $(4, 0)$. The maximum point on the curve is $(... show full transcript

Worked Solution & Example Answer:Figure 1 shows a sketch of the curve with equation $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 8 - 2008 - Paper 2

Step 1

a) $y = 2f(x)$

96%

114 rated

Answer

To sketch the graph of $y = 2f(x)$ , we start with the original function $f(x)$ . Since the maximum point at $(2, 5)$ is multiplied by 2, the new maximum point will be at $(2, 10)$ .

The curve will still intersect the x-axis at the same points, $(1, 0)$ and $(4, 0)$ . Therefore, the graph should look like this:

The maximum point at $(2, 10)$ .
The x-intercepts at $(1, 0)$ and $(4, 0)$ labelled clearly.

Step 2

b) $y = f(-x)$

99%

104 rated

Answer

For the graph of $y = f(-x)$ , we reflect the original graph across the y-axis. The maximum point's coordinates will change accordingly:

The maximum point of the reflected curve will now be at $(-2, 5)$ .
The curve will intersect the y-axis at $(-1, 0)$ and $(1, 0)$ .

Thus, the final graph will show:

Maximum point at $(-2, 5)$ .
X-intercepts at $(-1, 0)$ and $(1, 0)$ labelled clearly.

Step 3

c) Write down the value of the constant $a$

96%

101 rated

Answer

The value of the constant $a$ is 2, as it is mentioned that the maximum point on the curve $y = f(x + a)$ reflects the vertical scaling factor introduced by the $2$ from part (a). Therefore, it can be directly stated:

$a = 2$ .

Figure 1 shows a sketch of the curve with equation $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 8 - 2008 - Paper 2

Worked Solution & Example Answer:Figure 1 shows a sketch of the curve with equation $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 8 - 2008 - Paper 2

a) $y = 2f(x)$

b) $y = f(-x)$

c) Write down the value of the constant $a$

Join the A-Level students using SimpleStudy...