A-Level Edexcel Maths Pure Solving Equations: Figure 1 shows the graph of equa

Figure 1 shows the graph of equation $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 3 - 2012 - Paper 6

Question 3

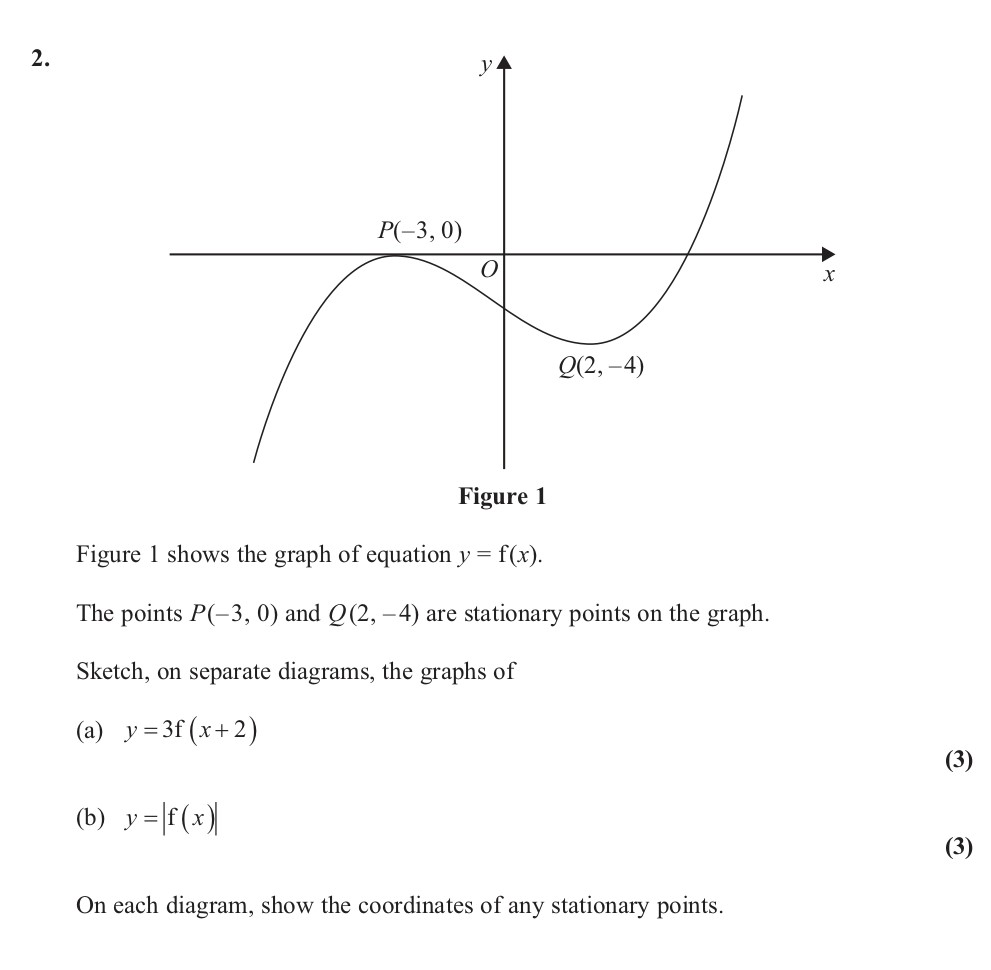
Figure 1 shows the graph of equation $y = f(x)$. The points $P(-3, 0)$ and $Q(2, -4)$ are stationary points on the graph. Sketch, on separate diagrams, the graph... show full transcript

Worked Solution & Example Answer:Figure 1 shows the graph of equation $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 3 - 2012 - Paper 6

Step 1

Sketch $y = 3f(x + 2)$

96%

114 rated

Answer

To sketch the graph of $y = 3f(x + 2)$ , follow these steps:

Understanding the Transformation: The expression $f(x + 2)$ indicates a horizontal shift of the graph of $f(x)$ to the left by 2 units. The factor of 3 in front of $f$ indicates a vertical stretch by a factor of 3.
Identifying Stationary Points: The stationary points of the original function are located at $P(-3, 0)$ and $Q(2, -4)$ . After shifting left by 2 units:
- Point $P$ moves to $(-5, 0)$ .
- Point $Q$ moves to $(0, -4)$ .
Applying the Vertical Stretch: Applying a vertical stretch of 3 will modify the y-coordinates of the stationary points:
- New point for $P$ : $(-5, 3 imes 0) = (-5, 0)$ .
- New point for $Q$ : $(0, 3 imes -4) = (0, -12)$ .
Drawing the Graph: Draw the transformed graph maintaining the shape of the original function while ensuring that the points $(-5, 0)$ and $(0, -12)$ are plotted correctly. Ensure the right section of the graph retains its characteristics as the original curve.

Step 2

Sketch $y = |f(x)|$

99%

104 rated

Answer

To sketch the graph of $y = |f(x)|$ , consider the following:

Understanding Absolute Values: The absolute value function, $|f(x)|$ , transforms any negative y-values of $f(x)$ to their positive counterparts, while keeping positive values unchanged.
Identifying and Transforming Points: For the original points:
- Stationary point $P(-3, 0)$ remains unchanged since $0$ is already non-negative.
- The stationary point $Q(2, -4)$ will change to $(2, 4)$ because we take the absolute value of $-4$ .
Plotting the Graph: The new graph will reflect any part of the original function that is below the x-axis across to above the x-axis. Draw the usual shape for the above points, noting that the portion of the graph between $(-3, 0)$ and $(2, -4)$ will be reflected to $(2, 4)$ .
Final Touches: Ensure that all curves and points are combined to reflect the effect of taking absolute values, clearly displaying the new coordinates of the stationary points at $P(-3, 0)$ and $Q(2, 4)$ .

Figure 1 shows the graph of equation $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 3 - 2012 - Paper 6

Worked Solution & Example Answer:Figure 1 shows the graph of equation $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 3 - 2012 - Paper 6

Sketch $y = 3f(x + 2)$

Sketch $y = |f(x)|$

Join the A-Level students using SimpleStudy...