Photo AI
(a) Show that \( \frac{(3-\sqrt{x})^3}{\sqrt{x}} \) can be written as \( 9x^{1/2} - 6x + x^{3/2} \) - Edexcel - A-Level Maths Pure - Question 7 - 2005 - Paper 1
Question 7
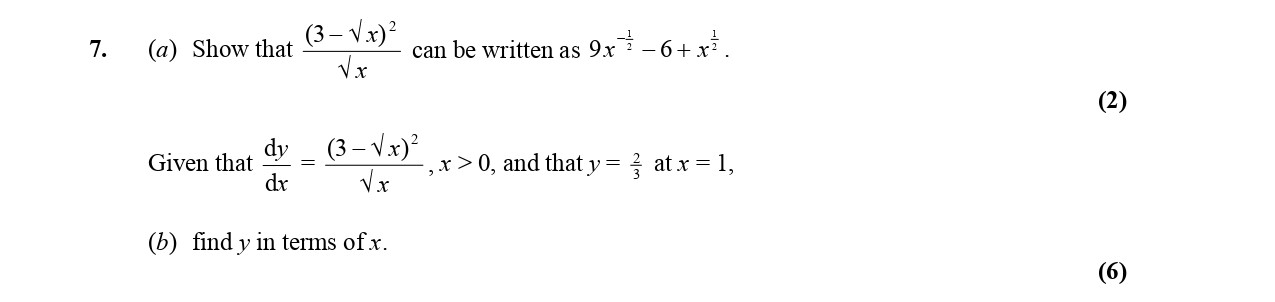
(a) Show that \( \frac{(3-\sqrt{x})^3}{\sqrt{x}} \) can be written as \( 9x^{1/2} - 6x + x^{3/2} \). Given that \( \frac{dy}{dx} = \frac{(3-\sqrt{x})^3}{\sqrt{x}} \... show full transcript
Worked Solution & Example Answer:(a) Show that \( \frac{(3-\sqrt{x})^3}{\sqrt{x}} \) can be written as \( 9x^{1/2} - 6x + x^{3/2} \) - Edexcel - A-Level Maths Pure - Question 7 - 2005 - Paper 1
Step 1
Show that \( \frac{(3-\sqrt{x})^3}{\sqrt{x}} \) can be written as \( 9x^{1/2} - 6x + x^{3/2} \)
Answer
To show the equivalence, we start with the expression ( \frac{(3-\sqrt{x})^3}{\sqrt{x}} ).
First, expand the numerator:
We then divide each term by ( \sqrt{x} ):
Rearranging, we get:
Thus, we have confirmed that the expression can be rewritten as required.
Step 2
find \( y \) in terms of \( x \)
Answer
Given ( \frac{dy}{dx} = \frac{(3-\sqrt{x})^3}{\sqrt{x}} ), we will integrate to find ( y ).
This implies:
Using the substitution, let ( u = \sqrt{x} ), then ( x = u^2 ) and ( dx = 2u , du ). The integral becomes:
Expanding ( (3-u)^3 ):
Thus, the integral becomes:
Now, substituting back ( u = \sqrt{x} ):
Next, we need to find the constant of integration ( c ) using the given condition ( y = \frac{1}{3} ) when ( x = 1 ):
This simplifies to:
Then solving for ( c ):
Finally, substitute ( c ) back into the equation:
This gives us ( y ) in terms of ( x ).
