Photo AI

Figure 2 shows a sketch of part of the curve with equation g(r) = x²(1 - x)e^{-2x}, \, x > 0 (a) Show that g'(x) = f(c)e^{-2x}, where f(c) is a cubic function to be found - Edexcel - A-Level Maths Pure - Question 8 - 2015 - Paper 3

Question 8

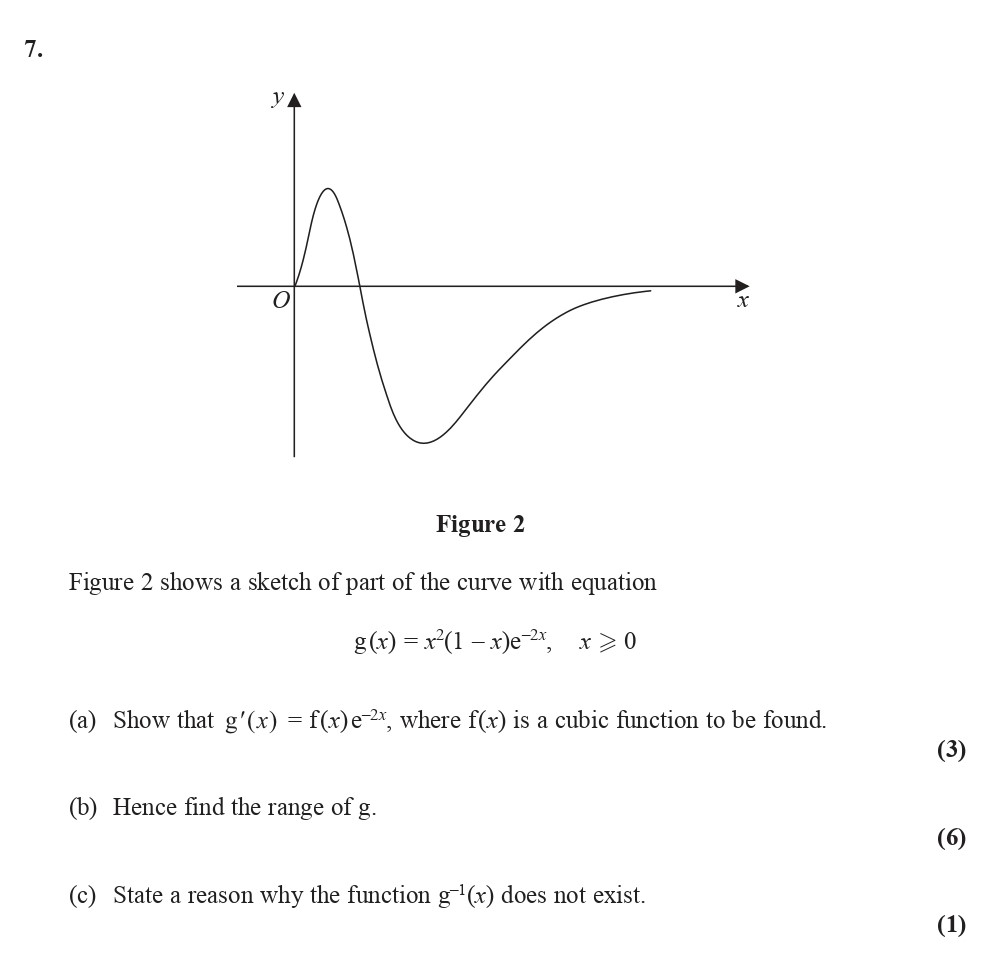
$Figure-2-shows-a-sketch-of-part-of-the-curve-with-equation--g(r)-=-x²(1---x)e^{-2x},-\,-x->-0--(a)-Show-that-g'(x)-=-f(c)e^{-2x},-where-f(c)-is-a-cubic-function-to-be-found-Edexcel-A-Level Maths Pure-Question 8-2015-Paper 3.png$

Figure 2 shows a sketch of part of the curve with equation g(r) = x²(1 - x)e^{-2x}, \, x > 0 (a) Show that g'(x) = f(c)e^{-2x}, where f(c) is a cubic function to b... show full transcript

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation g(r) = x²(1 - x)e^{-2x}, \, x > 0 (a) Show that g'(x) = f(c)e^{-2x}, where f(c) is a cubic function to be found - Edexcel - A-Level Maths Pure - Question 8 - 2015 - Paper 3

Step 1

Show that g'(x) = f(c)e^{-2x}, where f(c) is a cubic function to be found.

96%

114 rated

Answer

To find the derivative of g, we apply the product rule:

Let g(x) = x²(1 - x)e^{-2x}.

Using the product rule:

$g'(x) = (x²(1 - x))' e^{-2x} + x²(1 - x) (e^{-2x})'$

Calculating the derivatives individually:

For the first term:
- $(x²(1 - x))' = 2x(1 - x) + x²(-1) = 2x - 3x²$ .
For the second term:
- $(e^{-2x})' = -2e^{-2x}$ .

Combining the product rule results gives:

$g'(x) = (2x - 3x²)e^{-2x} - 2x²(1 - x)e^{-2x}.$

Simplifying: $g'(x) = (2x - 3x² - 2x² + 2x³)e^{-2x} = (2x - 5x² + 2x³)e^{-2x}$

This expression can be represented as f(c) where f(c) is a cubic function. Therefore, we have shown the required relationship.

Step 2

Hence find the range of g.

99%

104 rated

Answer

To find the range of g(x) = x²(1 - x)e^{-2x}, we first need to identify the maximum point on this function.

The function is defined for x > 0.
We can find the critical points by setting g'(x) = 0: $2x - 5x² + 2x³ = 0 \Rightarrow x(2 - 5x + 2x²) = 0.$ Ignoring x = 0, we solve the quadratic $2 - 5x + 2x² = 0$ .
Using the quadratic formula: $x = \frac{-b \pm \sqrt{b² - 4ac}}{2a} = \frac{5 \pm \sqrt{(-5)² - 4(2)(2)}}{2(2)} = \frac{5 \pm \sqrt{25 - 16}}{4} = \frac{5 \pm 3}{4}.$ Thus, $x = 2$ and $x = \frac{1}{2}$ .
Evaluating g(2) and g(1/2):
- g(2) = 0 because of the term $(1 - 2)$ ;
- g(1/2) = (1/4)(1/2)e^{-1} = \frac{1}{8e}.
As x approaches 0, g(x) approaches 0.
- Hence, the range of g is: $0 \leq g(x) \leq \frac{1}{8e}.$ Therefore, the range is $[0, \frac{1}{8e}]$ .

Step 3

State a reason why the function g^{-1}(r) does not exist.

96%

101 rated

Answer

The function g(x) is not a one-to-one function because it is a many-to-one function. This means that there are multiple values of x that yield the same value of g(x). Since g(x) can take the same output for different inputs, it does not meet the criteria for the existence of an inverse function. Therefore, g^{-1}(r) does not exist.

Figure 2 shows a sketch of part of the curve with equation g(r) = x²(1 - x)e^{-2x}, \, x > 0 (a) Show that g'(x) = f(c)e^{-2x}, where f(c) is a cubic function to be found - Edexcel - A-Level Maths Pure - Question 8 - 2015 - Paper 3

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation g(r) = x²(1 - x)e^{-2x}, \, x > 0 (a) Show that g'(x) = f(c)e^{-2x}, where f(c) is a cubic function to be found - Edexcel - A-Level Maths Pure - Question 8 - 2015 - Paper 3

Show that g'(x) = f(c)e^{-2x}, where f(c) is a cubic function to be found.

Hence find the range of g.

State a reason why the function g^{-1}(r) does not exist.

Join the A-Level students using SimpleStudy...