The curve with equation $y = 3 \, ext{sin} \, \frac{x}{2}$, $0 \leq x \leq 2\pi$, is shown in Figure 1. The finite region enclosed by the curve and the x-axis is shaded. (a) Find, by integration, the area of the shaded region. This region is rotated through $2\pi$ radians about the x-axis. (b) Find the volume of the solid generated.

A-Level Edexcel Maths Pure Vectors in 3 Dimensions: The curve with equation $y = 3 \

The curve with equation $y = 3 \, ext{sin} \, \frac{x}{2}$, $0 \leq x \leq 2\pi$, is shown in Figure 1 - Edexcel - A-Level Maths Pure - Question 5 - 2006 - Paper 6

Question 5

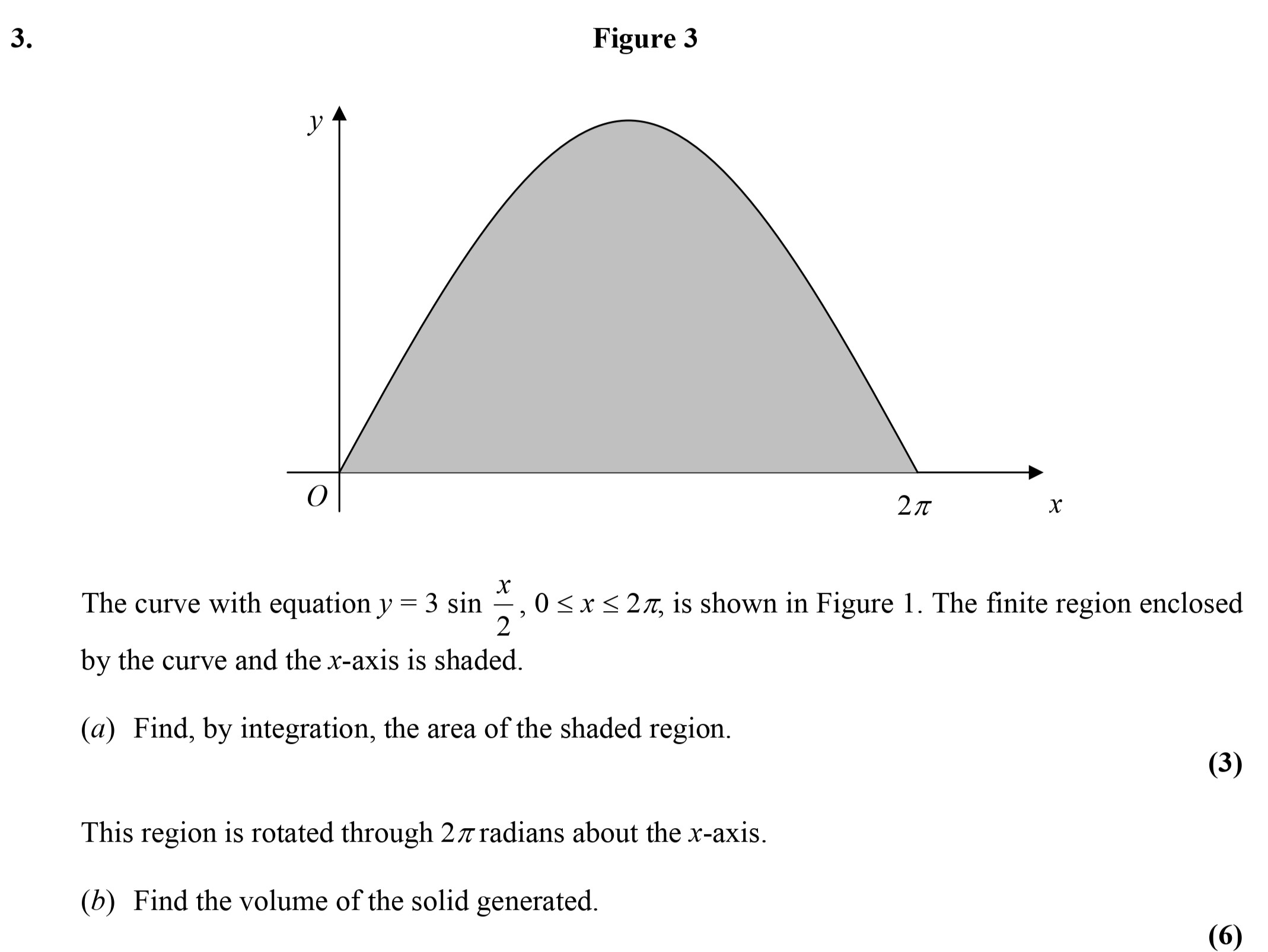
$The-curve-with-equation-$y-=-3-\,--ext{sin}-\,-\frac{x}{2}$,-$0-\leq-x-\leq-2\pi$,-is-shown-in-Figure-1-Edexcel-A-Level Maths Pure-Question 5-2006-Paper 6.png$

The curve with equation $y = 3 \, ext{sin} \, \frac{x}{2}$, $0 \leq x \leq 2\pi$, is shown in Figure 1. The finite region enclosed by the curve and the x-axis is sh... show full transcript

Worked Solution & Example Answer:The curve with equation $y = 3 \, ext{sin} \, \frac{x}{2}$, $0 \leq x \leq 2\pi$, is shown in Figure 1 - Edexcel - A-Level Maths Pure - Question 5 - 2006 - Paper 6

Step 1

Find, by integration, the area of the shaded region.

96%

114 rated

Answer

To find the area of the shaded region, we will integrate the function from $0$ to $2\pi$ :

$A = \int_0^{2\pi} 3\sin\left(\frac{x}{2}\right) \, dx$

Calculating the integral:

First, we find the antiderivative:

$A = -6\cos\left(\frac{x}{2}\right) \bigg|_0^{2\pi}$

Evaluating this from $0$ to $2\pi$ gives:

$A = -6\cos\left(\frac{2\pi}{2}\right) - (-6\cos(0)) = -6\cos(\pi) + 6\cos(0)$ $= -6(-1) + 6(1) = 6 + 6 = 12$

Thus, the area of the shaded region is $12$ square units.

Step 2

Find the volume of the solid generated.

99%

104 rated

Answer

To find the volume generated by rotating the shaded area about the x-axis, we use the formula for the volume of revolution:

$V = \pi \int_0^{2\pi} \left(3\sin\left(\frac{x}{2}\right)\right)^2 \, dx$

Simplifying the expression:

$= 9\pi \int_0^{2\pi} \sin^2\left(\frac{x}{2}\right) \, dx$

Using the identity for $\\sin^2$ : $\\sin^2(A) = \frac{1 - \cos(2A)}{2}$

We play this identity: $V = 9\pi \int_0^{2\pi} \frac{1 - \cos(x)}{2} \, dx$

Calculating the integral: That's: $V = \frac{9\pi}{2} \left[ x - \sin(x) \right]_0^{2\pi}$

Evaluating the integral from $0$ to $2\pi$ results in:

$V = \frac{9\pi}{2} \left[ (2\pi - 0) - (0 - 0) \right] = \frac{9\pi}{2} (2\pi) = \frac{9\pi^2}{2}$

Calculating the numerical value: $V \approx 9 \cdot \frac{3.14159^2}{2} \approx 9 \cdot 4.9348 \approx 44.51$

Thus, the volume of the solid generated is approximately $44.51$ cubic units.

The curve with equation $y = 3 \, ext{sin} \, \frac{x}{2}$, $0 \leq x \leq 2\pi$, is shown in Figure 1 - Edexcel - A-Level Maths Pure - Question 5 - 2006 - Paper 6

Worked Solution & Example Answer:The curve with equation $y = 3 \, ext{sin} \, \frac{x}{2}$, $0 \leq x \leq 2\pi$, is shown in Figure 1 - Edexcel - A-Level Maths Pure - Question 5 - 2006 - Paper 6

Find, by integration, the area of the shaded region.

Find the volume of the solid generated.

Join the A-Level students using SimpleStudy...