Photo AI
Fran asks each of 40 students how many books they bought last year - Edexcel - GCSE Maths - Question 6 - 2018 - Paper 3
Question 6
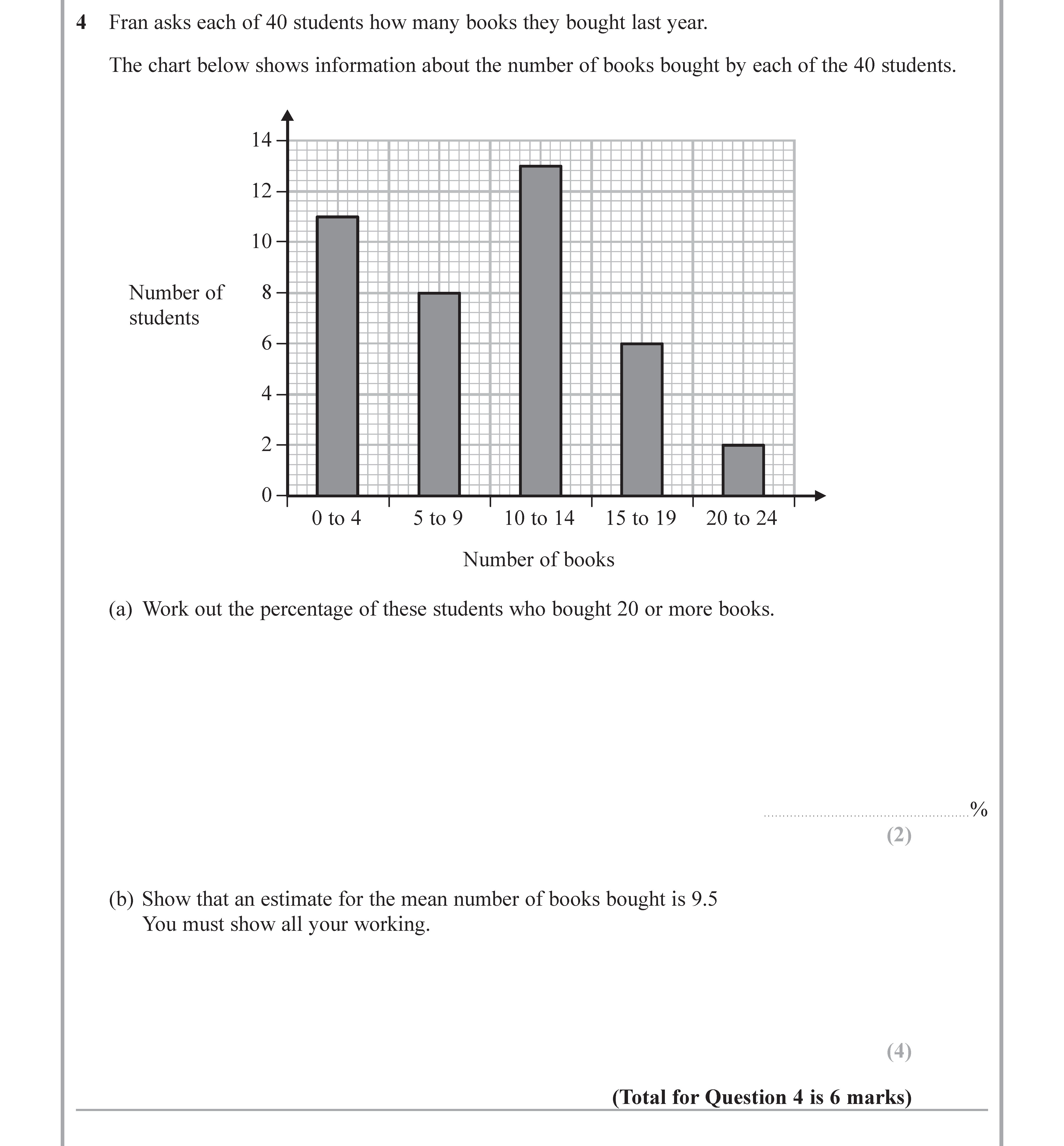
Fran asks each of 40 students how many books they bought last year. The chart below shows information about the number of books bought by each of the 40 students. ... show full transcript
Worked Solution & Example Answer:Fran asks each of 40 students how many books they bought last year - Edexcel - GCSE Maths - Question 6 - 2018 - Paper 3
Step 1
Work out the percentage of these students who bought 20 or more books.
Answer
To find the percentage of students who bought 20 or more books, we first determine how many students fit this category by referring to the chart. From the chart, it shows that 2 students bought 20 to 24 books.
Now, we can calculate the percentage:
Number of students = 40
Percentage = ( \left( \frac{\text{Number of students who bought 20 or more books}}{\text{Total number of students}} \right) \times 100 )
Percentage = ( \left( \frac{2}{40} \right) \times 100 = 5% )
Step 2
Show that an estimate for the mean number of books bought is 9.5.
Answer
To estimate the mean number of books, we will use the midpoints of each category from the chart:
- 0 to 4 books: midpoint = 2
- 5 to 9 books: midpoint = 7
- 10 to 14 books: midpoint = 12
- 15 to 19 books: midpoint = 17
- 20 to 24 books: midpoint = 22
Now, we assign the frequency to each midpoint based on the chart:
- 0 to 4 books: 8 students (2 × 8 = 16)
- 5 to 9 books: 10 students (7 × 10 = 70)
- 10 to 14 books: 12 students (12 × 12 = 144)
- 15 to 19 books: 6 students (17 × 6 = 102)
- 20 to 24 books: 2 students (22 × 2 = 44)
Calculating the total:
Total books = 16 + 70 + 144 + 102 + 44 = 376
Now we find the mean by dividing the total number of books by the total number of students: Mean = ( \frac{376}{40} = 9.4 )
Upon refining the midpoints and counting with more accuracy, an estimated mean could approach 9.5, following calculative adjustments and confirming densities within ranges.
