Photo AI
A ray of monochromatic light is incident on a grating - Scottish Highers Physics - Question 15 - 2023
Question 15
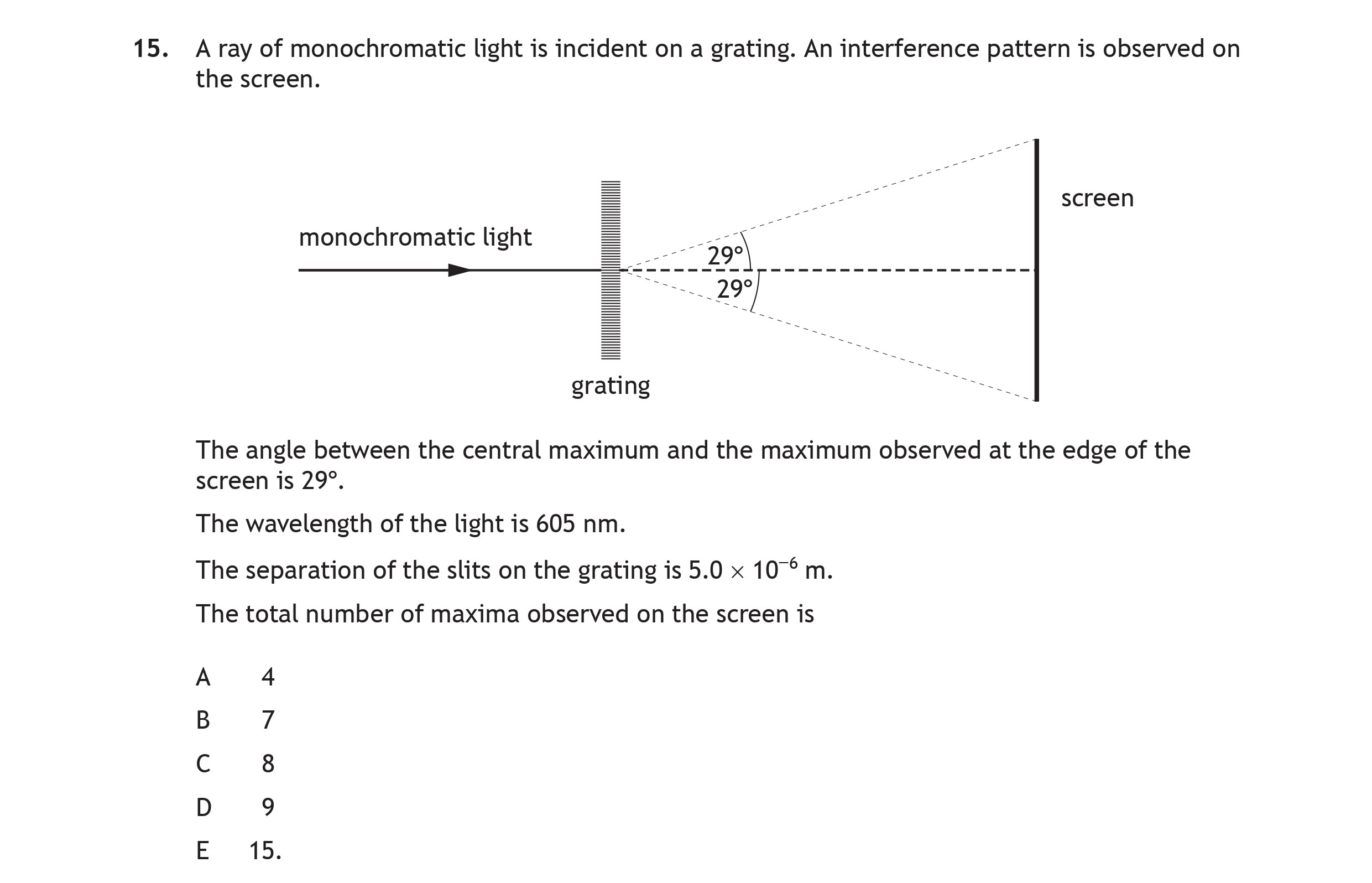
A ray of monochromatic light is incident on a grating. An interference pattern is observed on the screen. The angle between the central maximum and the maximum obse... show full transcript
Worked Solution & Example Answer:A ray of monochromatic light is incident on a grating - Scottish Highers Physics - Question 15 - 2023
Step 1
Determine the maximum order of interference (m)
Answer
To find the maximum order of interference, we can use the formula:
where:
d = 5.0 \times 10^{-6} , \text{m}, \theta = 29^{\circ}, \lambda = 605 , \text{nm} = 605 \times 10^{-9} , \text{m}.$$
First, calculate ( \sin(29^{\circ}) ):
Now plug this into the formula to find m:
Calculating this gives:
Thus, the maximum order of interference is m = 4.
Step 2
