Area

A Quick Word About Area

Calculating the area of shapes is an essential skill in Maths, and it's straightforward as long as you remember the formulas! These formulas are often provided in exams, but sometimes you need to know them by heart. Here's a crucial point to remember:

Always give your answer in squared units! This means if the measurements are in metres, your area should be in $m^2$ ; if they are in centimetres, then $cm^2$ , and so on.

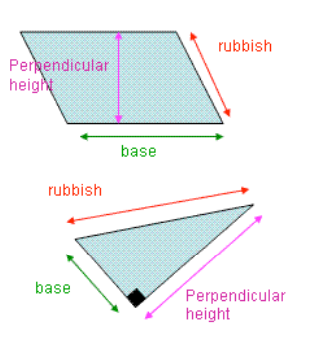
The Importance of Perpendicular Height

When calculating the area of many shapes, you'll need to multiply the base by the height. However, it's not just any height—it must be the perpendicular height.

What is Perpendicular Height?

The height must be perpendicular to the base. This means the height you measure must form a right angle ( $90°$ ) with the base.
If the base is horizontal (flat), then the height should be vertical (straight up), not a slanted line. A slanted height might be given to confuse you, but it's not the height you use to calculate the area.

1. Area of a Rectangle

The area of a rectangle is found by multiplying its base (width) by its height (length).

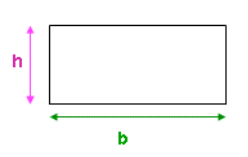
Formula:

Area=b×h

Where:

$b$ is the base (width) of the rectangle.
$h$ is the height (length) of the rectangle.

infoNote

Example:

Given: A rectangle with a base of $3$ cm and a height of $9$ cm.
Calculation:

Area=3\ cm×9 \ cm=27\ cm^2

Answer: The area of the rectangle is $27 \ cm^2$ . Steps:

Identify the base $b$ and height $h$ of the rectangle.
Multiply the base by the height.
The result is the area in squared units.

2. Area of a Triangle

The area of a triangle is calculated by multiplying the base by the perpendicular height and then dividing by $2$ .

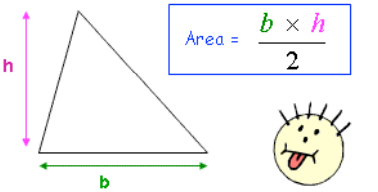
Formula:

Area=\frac{b×h}2

Where:

$b$ is the base of the triangle.
$h$ is the perpendicular height (the height must be at a right angle to the base).

infoNote

Example:

Given: A triangle with a base of $10$ m and a perpendicular height of $12$ m.
Calculation:

Area=\frac{10 \ m×12\ m}2=\frac{120\ m^2}2=60\ m^2

Answer: The area of the triangle is $60 \ m^2$ . Steps:

Identify the base $b$ and the perpendicular height $h$ of the triangle.
Multiply the base by the height.
Divide the result by $2$ to find the area in squared units.

3. Area of a Parallelogram

The area of a parallelogram is similar to that of a rectangle. You multiply the base by the perpendicular height. Remember, the height must be perpendicular to the base, not slanted.

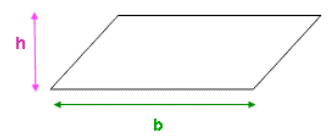
Formula:

Area=b×h

Where:

$b$ is the base of the parallelogram.
$h$ is the perpendicular height.

infoNote

Example:

Given: A parallelogram with a base of $5$ mm and a perpendicular height of $10$ mm.
Calculation:

Area=5 \ mm×10\ mm=50\ mm^2

Answer: The area of the parallelogram is $50 \ mm^2$ . Steps:

Identify the base $b$ and the perpendicular height $h$ .
Multiply the base by the height.
The result gives the area in squared units.

4. Area of a Trapezium

The area of a trapezium is calculated by taking the average of the lengths of the two parallel sides (often called the bases) and then multiplying by the height. This method effectively finds the "average" base length and then applies the standard base $×$ height calculation.

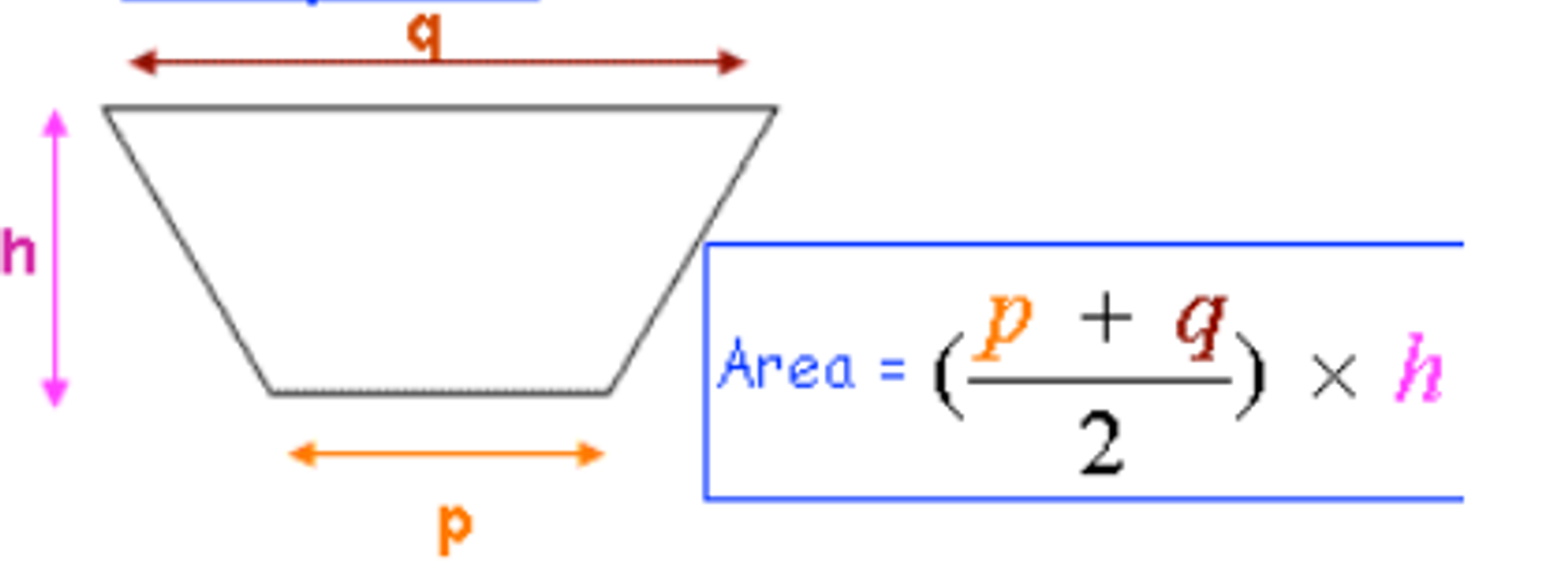
Formula:

Area=\frac{(p+q)}2×h

Where:

$p$ and $q$ are the lengths of the parallel sides.
$h$ is the perpendicular height.

infoNote

Example:

Given: A trapezium with parallel sides measuring $2.8$ cm and $4.2$ cm, and a height of $8$ cm.
Calculation:

Area=\frac{(2.8 \ cm+4.2 cm)}2×8\ cm

Area=\frac{7 \ cm}2×8\ cm=3.5\ cm×8 \ cm=28 \ cm^2

Answer: The area of the trapezium is $28 \ cm^2$ . Steps:

Add the lengths of the parallel sides $p$ and $q$ .
Divide the sum by $2$ to get the average length of the base.
Multiply the average base length by the height $h$ .
The result is the area in squared units.

5. Area of a Kite

The area of a kite can be found by multiplying the lengths of its diagonals (the two lines that cross each other from one corner of the kite to the other).

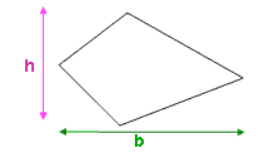
Formula:

Area=\frac12×d₁×d₂

Where:

$d₁$ and $d₂$ are the lengths of the diagonals of the kite.

infoNote

Example:

Given: A kite with diagonals of $2.5$ m and $4$ m.
Calculation:

Area=\frac{1}2×2.5\ m×4\ m=\frac{1}2×10\ m^2=5\ m^2

Answer: The area of the kite is $5 \ m^2$ . Steps:

Measure or identify the lengths of the diagonals $d₁$ and $d₂$ .
Multiply these lengths together.
Divide the product by $2$ to get the area in squared units.

6. Area of a Circle

The area of a circle is calculated using the radius, which is half the diameter of the circle. You square the radius and multiply it by the mathematical constant π_π_ (approximately $3.14159$ ).

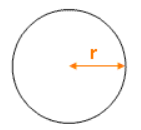
Formula:

Area=π×r^2

Where:

$r$ is the radius of the circle.

infoNote

Example:

Given: A circle with a diameter of $12.6\ m$ .
Calculation:
First, find the radius: $r=\frac{12.6 m}2=6.3\ m.$

Area=π×6.3^2=π×39.69 \ m^2≈124.7 \ m^2 \ (to\ 1\ decimal\ place)

Answer: The area of the circle is approximately $124.7 \ m^2$ . Steps:

If given the diameter, halve it to find the radius $r$ .
Square the radius $r^2$ .
Multiply the squared radius by $π$ to find the area in squared units.

Compound Area: Breaking Down Complex Shapes

Key Concept:

Compound shapes are made up of simpler shapes. To find the total area, split the compound shape into familiar shapes (like rectangles, triangles, or trapeziums), calculate the area of each part, and then add those areas together.

infoNote

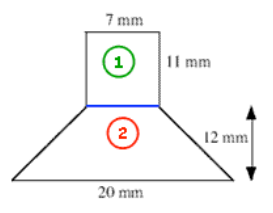
Worked Example: Finding the Area of a Compound Shape

Problem: You are given a compound shape made up of a rectangle and a trapezium. You need to find the total area of the shape.

Step 1: Identify and Split the Compound Shape

The shape can be divided into:

Rectangle
Trapezium

Step 2: Calculate the Area of Each Shape

Rectangle (Shape $1$ )

Given:

Base $b=7 \ mm$
Height $h=11 mm$

Formula:

Area of Rectangle=b×h

Calculation:

Area=7 \ mm×11 \ mm=77\ mm^2

Trapezium (Shape $2$ ) Given:

Parallel sides $p=20 mm$ and $q=7 mm$
Height $h=12 mm$

Formula:

Area\ of\ Trapezium=\frac{(p+q)}2×h

Calculation:

$Area=\frac{(20\ mm+7\ mm)}2×12 \ mm=\frac{27 \ mm}2×12\ mm=13.5 \ mm×12\ mm=162 \ mm^2$

Step 3: Add the Areas Together

Total Area:

Total Area=Area of Rectangle+Area of Trapezium

Total\ Area=77\ mm^2+162\ mm^2=239\ mm^2

Answer: The total area of the compound shape is $239 \ mm^2$ .

Understanding Surface Area

Key Concept:

Surface area is the sum of the areas of all the faces of a $3D$ object. Each face is a $2D$ shape, and the surface area is calculated by adding the areas of these individual shapes.

infoNote

Worked Example: Calculating Surface Area

Let's consider a $3D$ object that is composed of several simpler shapes. The task is to calculate the total surface area of this object.

Step 1: Identify and Label Each Face

Break the 3D object into simpler $2D$ shapes:

Triangle (Shape $1$ )
Rectangle (Shape $2$ )
Rectangle (Shape $3$ )
Rectangle (Shape $4$ )
Triangle (Shape $5$ )

Step 2: Calculate the Area of Each Face

Triangle (Shape $1$ )

Given: Base $b=6 cm$ , Height $h=8 cm$
Formula:

Area \ of \ Triangle=\frac{b×h}2

Calculation:

Area=\frac{6\ cm×8 \ cm}2=\frac{48 \ cm^2}2=24 \ cm^2

Rectangle (Shape $2$ )

Given: Length $l=10 cm$ , Width $w=2 cm$
Formula:

Area of Rectangle=l×w

Calculation:

Area=10 \ cm×2 \ cm=20 \ cm^2

Rectangle (Shape $3$ )

Given: Length $l=2 cm$ , Width $w=6 cm$
Formula:

Area of Rectangle=l×w

Calculation:

Area=2 \ cm×6\ cm=12\ cm^2

Rectangle (Shape $4$ )

Given: Length $l=8 cm$ , Width $w=2 cm$
Formula:

Area of Rectangle=l×w

Calculation:

Area=8 \ cm×2 \ cm=16 \ cm^2

Triangle (Shape $5$ )

Given: This triangle is the same as Shape $1$ .
Area:

Area=24 \ cm^2

Step 3: Add the Areas Together

Total Surface Area:

Total Area=Area of Shape 1+Area of Shape 2+Area of Shape 3+Area of Shape 4+Area of Shape 5

Total Area=24 \ cm^2+20 \ cm^2+12 \ cm^2+16 \ cm^2+24 \ cm^2=96 \ cm^2

Answer: The total surface area of the shape is $96\ cm^2$ .

Area Simplified Revision Notes for GCSE OCR Maths

Area

A Quick Word About Area

The Importance of Perpendicular Height

What is Perpendicular Height?

1. Area of a Rectangle

2. Area of a Triangle

3. Area of a Parallelogram

4. Area of a Trapezium

5. Area of a Kite

6. Area of a Circle

Compound Area: Breaking Down Complex Shapes

Worked Example: Finding the Area of a Compound Shape

Step 1: Identify and Split the Compound Shape

Step 2: Calculate the Area of Each Shape

Step 3: Add the Areas Together

Understanding Surface Area

Worked Example: Calculating Surface Area

500K+ Students Use These Powerful Tools to Master Area For their GCSE Exams.

Other Revision Notes related to Area you should explore