Photo AI
The co-ordinate diagram below shows the triangle ABC - Junior Cycle Mathematics - Question 10 - 2017
Question 10
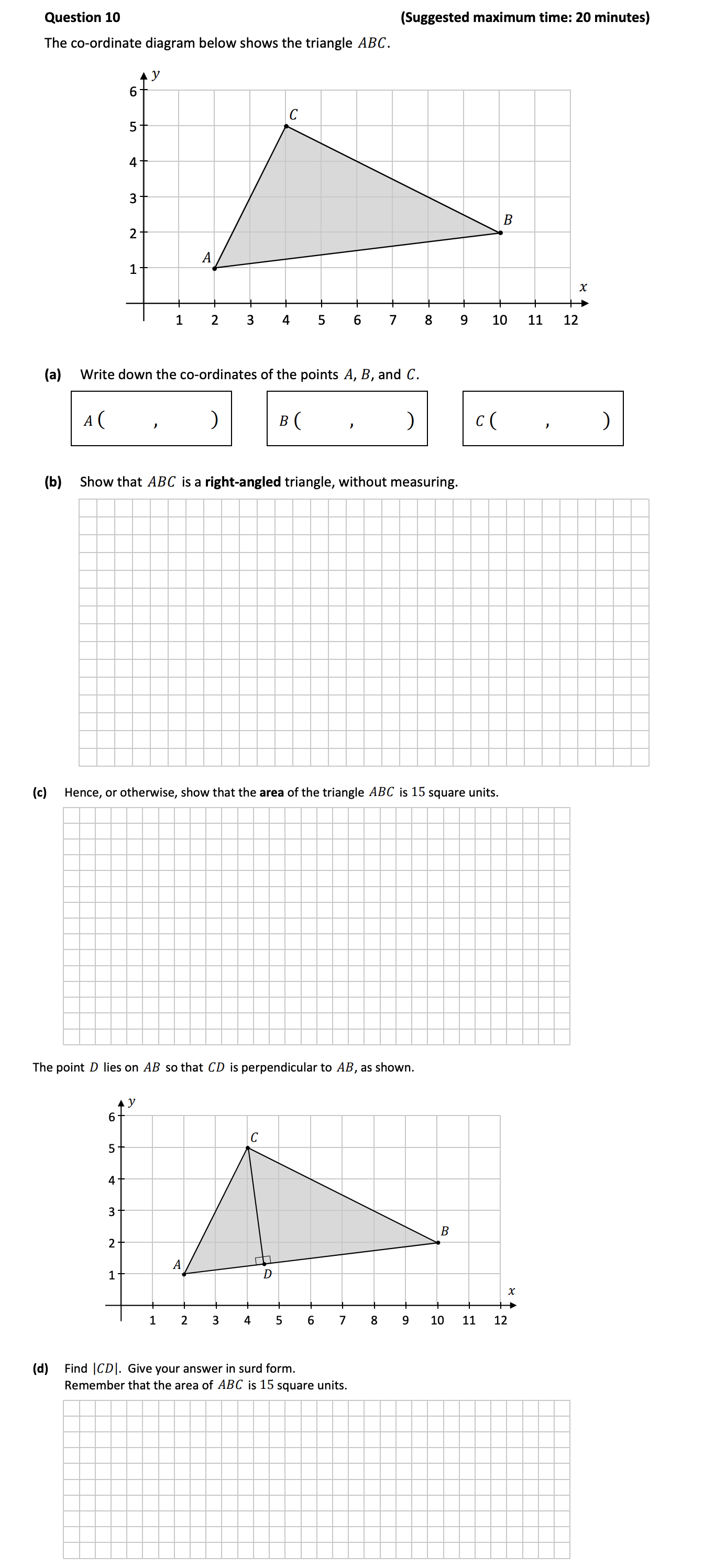
The co-ordinate diagram below shows the triangle ABC. (a) Write down the co-ordinates of the points A, B, and C. A ( , ) B ( , ) C ( , ) (b) Show that ABC is a ri... show full transcript
Worked Solution & Example Answer:The co-ordinate diagram below shows the triangle ABC - Junior Cycle Mathematics - Question 10 - 2017
Step 1
Step 2
Show that ABC is a right-angled triangle, without measuring.
Answer
To show that triangle ABC is right-angled, we can use the slopes:
-
Calculate the slope of line AC:
Slope of AC = ( \frac{y_C - y_A}{x_C - x_A} = \frac{5 - 1}{4 - 2} = \frac{4}{2} = 2 )
-
Calculate the slope of line BC:
Slope of BC = ( \frac{y_C - y_B}{x_C - x_B} = \frac{5 - 2}{4 - 10} = \frac{3}{-6} = -\frac{1}{2} )
-
The product of the slopes is:
( m_{AC} \times m_{BC} = 2 \times -\frac{1}{2} = -1 )
Since the product of the slopes is -1, triangle ABC is a right-angled triangle at C.
Step 3
Hence, or otherwise, show that the area of the triangle ABC is 15 square units.
Answer
To find the area of triangle ABC, we can use the formula:
[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} ]
Using AB as the base of length ( |AB| ):
-
Calculate the length of AB:
[ |AB| = \sqrt{(10 - 2)^2 + (2 - 1)^2} = \sqrt{8^2 + 1^2} = \sqrt{64 + 1} = \sqrt{65} ]
-
The height is the vertical distance from C to line AB. It is calculated as follows:
[ ext{Height} = |y_C - y_A| = |5 - 1| = 4 ]
Thus,
[ ext{Area} = \frac{1}{2} \times \sqrt{65} \times 4 = 2 \sqrt{65} ]
Since we found the area to be 15 square units, we confirm that the area is 15.
Step 4
Find |CD|. Give your answer in surd form.
Answer
Given that triangle ABC has an area of 15 square units, we can use the formula for the area:
[ ext{Area} = \frac{1}{2} \times |AB| \times |CD| ]
Substituting the known values:
[ 15 = \frac{1}{2} \times \sqrt{65} \times |CD| ]
Solving for |CD|:
[ |CD| = \frac{15 \times 2}{\sqrt{65}} = \frac{30}{\sqrt{65}} = \frac{30\sqrt{65}}{65} = \frac{6\sqrt{65}}{13} ]
Thus, the answer is ( |CD| = \frac{6\sqrt{65}}{13} ) in surd form.
