Photo AI
4. (a) Two particles of masses 2 kg and 3 kg are connected by a taut, light, inextensible string which passes over a smooth light pulley - Leaving Cert Applied Maths - Question 4 - 2012
Question 4
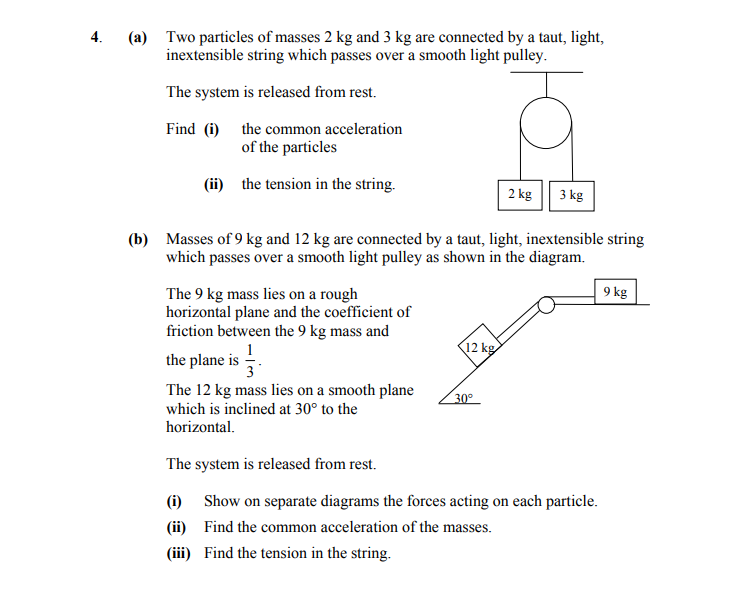
4. (a) Two particles of masses 2 kg and 3 kg are connected by a taut, light, inextensible string which passes over a smooth light pulley. The system is released fro... show full transcript
Worked Solution & Example Answer:4. (a) Two particles of masses 2 kg and 3 kg are connected by a taut, light, inextensible string which passes over a smooth light pulley - Leaving Cert Applied Maths - Question 4 - 2012
Step 1
(i) the common acceleration of the particles
Answer
To find the common acceleration of the particles, we can set up the equations of motion. For the 3 kg mass,
For the 2 kg mass,
Combining these equations, we can substitute from the second equation into the first. From the first equation, we get:
Substituting this into the second equation leads to:
This simplifies to:
So, we find:
Using , we have:
Step 2
Step 3
(i) Show on separate diagrams the forces acting on each particle
Answer
For the 9 kg mass on a rough horizontal plane:
- Weight () acting downwards.
- Normal force () acting upwards.
- Frictional force ( rac{1}{3}R) acting to the left.
- Tension () acting to the right.
For the 12 kg mass on a smooth plane:
- Weight () acting downwards.
- Normal force () acting perpendicular to the plane.
- Tension () acting upwards along the string.
Step 4
Step 5
